您的购物车目前是空的!
123

1.万能近似定理
-
每个前馈神经网络的
层可以看成是一个线性函数和非线性激活函数的组合。
-
为什么
线性函数+非线性激活函数的组合可以拟合任意的函数?
-
1989年,数学家乔治・西本科(
George Cybenko)通过严格的数学推导证明,提出了著名的万能近似定理(Universal Approximation Theorem)。
万能近似定理:只要神经元的数量足够多,每个神经元使用
线性函数和非线性激活函数的组合,可以逼近任意连续的函数(在有限区间上),无论目标函数多么复杂。
-
具体证明过程比较复杂,需要多个数学工具,这里不展开,通过图表了解一下具体的原理:
-
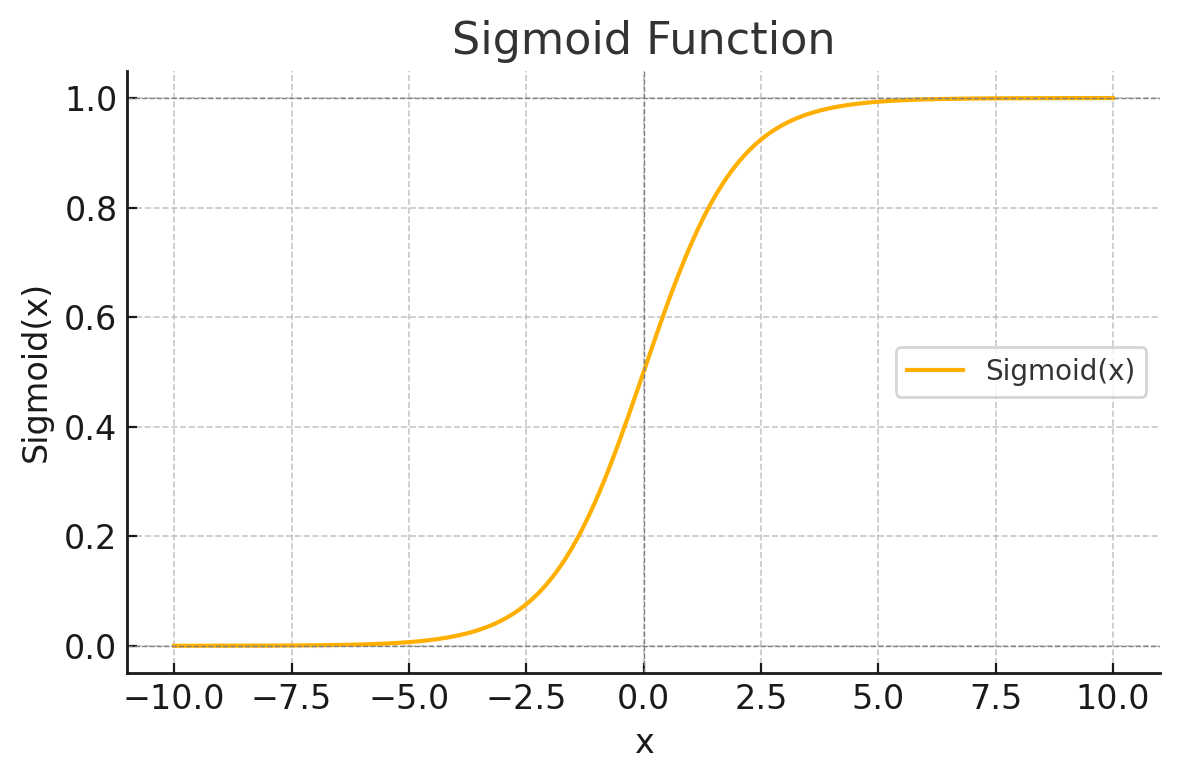
George Cybenko使用Sigmoid激活函数进行的证明,Sigmoid函数:
-
$$\tag1 Sigmoid(x) = \frac{1}{1+e^{-x}}$$
-
-
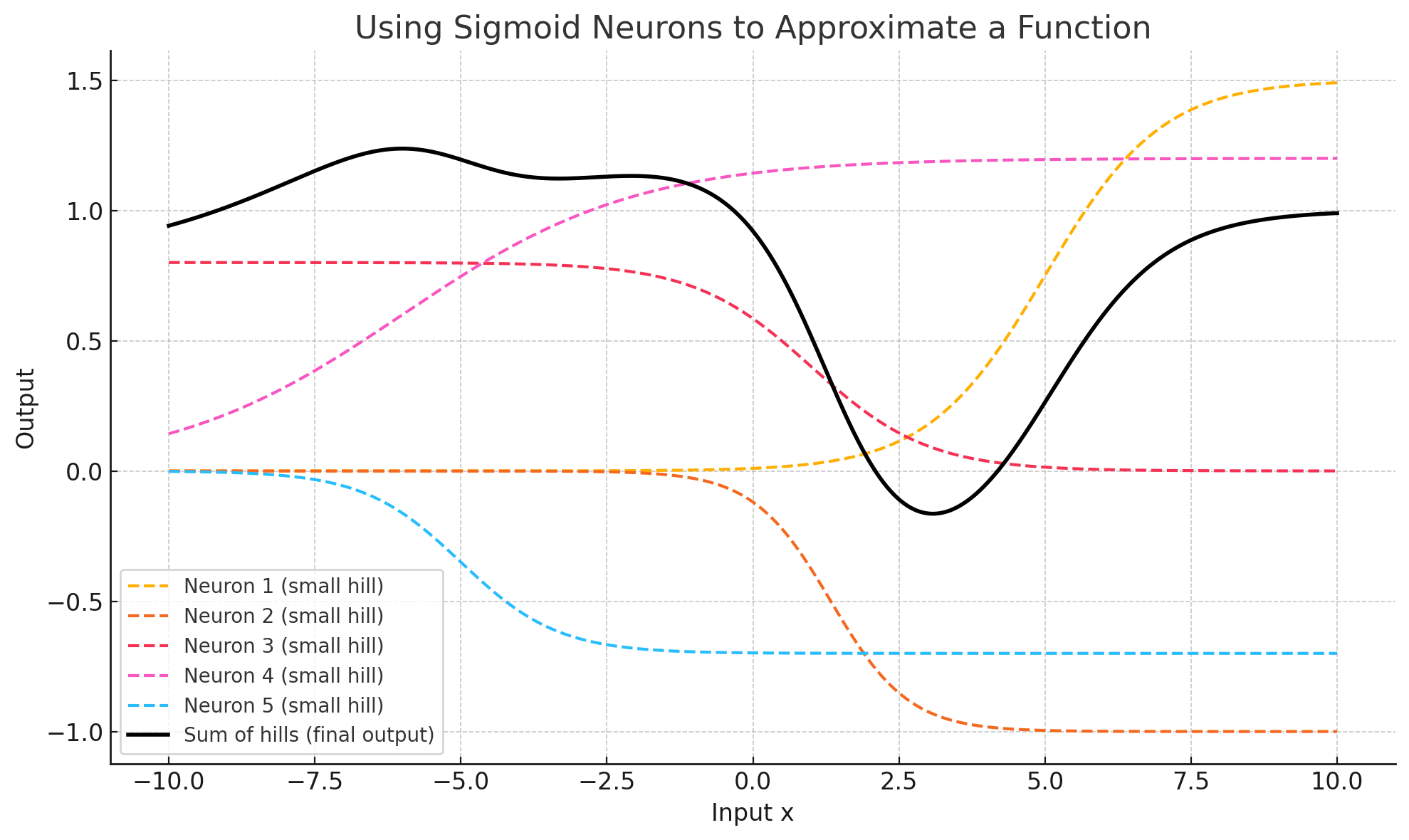
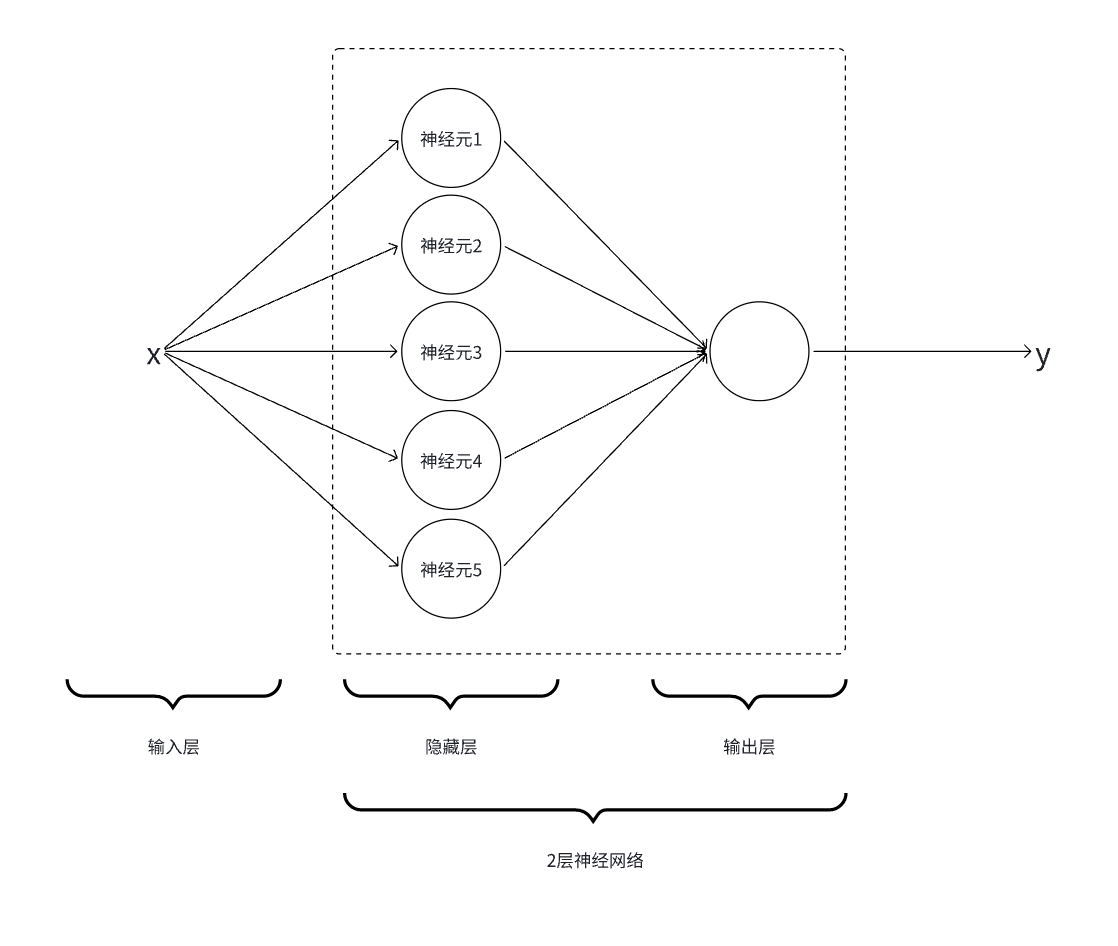
前馈神经网络中
每个层的每个神经元可以看成是一个Sigmoid函数进行线性变换(缩放、位移)的结果,而最终的输出y是所有Sigmoid函数的结果的相加。 -
下图所示,使用5个线性变化后的
Sigmoid函数拟合出复杂的目标函数。
-
前馈神经网络中
-
-
从上面的图表可以直观的感知到,不论多么复杂的曲线(目标函数),只要神经元足够多,通过多个
sigmoid函数的叠加(相加)都可以精准的表述出来。
-
从上面的图表可以直观的感知到,不论多么复杂的曲线(目标函数),只要神经元足够多,通过多个
2.图表表示训练过程
2.1.样本数据
-
已知的(x、y)数据对,下图表示输入数据
x只有一个特征,输出数据y只有一个特征。
2.2.求解目标
-
根据样本数据需要寻找的目标函数,如下图所示,是一个
x、y坐标的非线性曲线。 - 求解目标函数是未知的,下图只是用于示意。
2.3.设计网络结构
-
一个隐藏层:使用5个【线性函数+
Sigmoid激活函数】的组合,每个组合即一个神经元。 - 一个输出层:将隐藏层的5个神经元的结果进行合并相加。
2.4.迭代训练
-
第1次迭代:随机
初始化5个【线性函数+Sigmoid激活函数】的参数。- 下图只是用于示意,表示5个随机初始化的函数曲线叠加后的曲线。
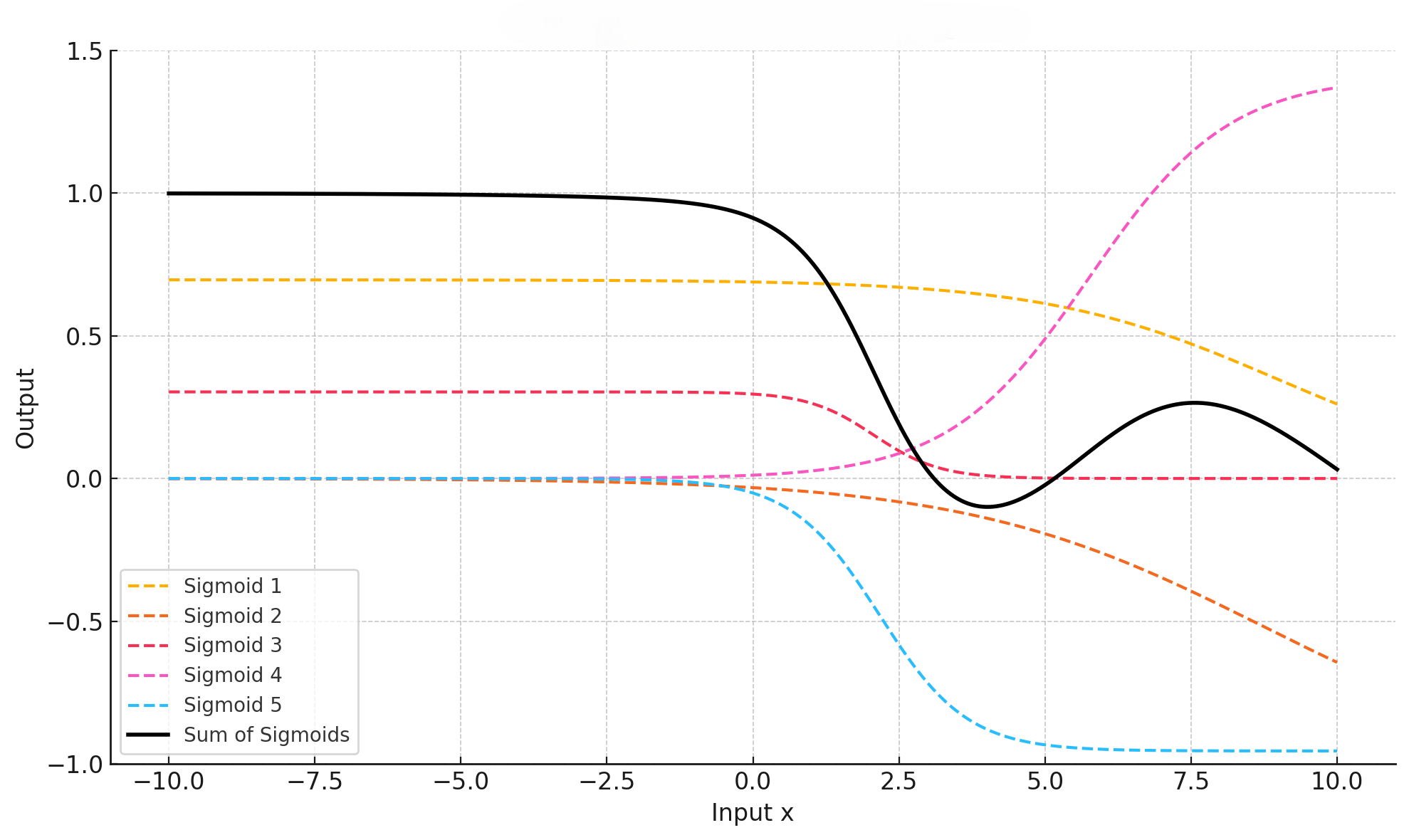
-
第2次迭代:基于第1次迭代的结果对参数进行调整,再次迭代。
- 下图只用于示意,可以发现图像在逐步往最优解变化。
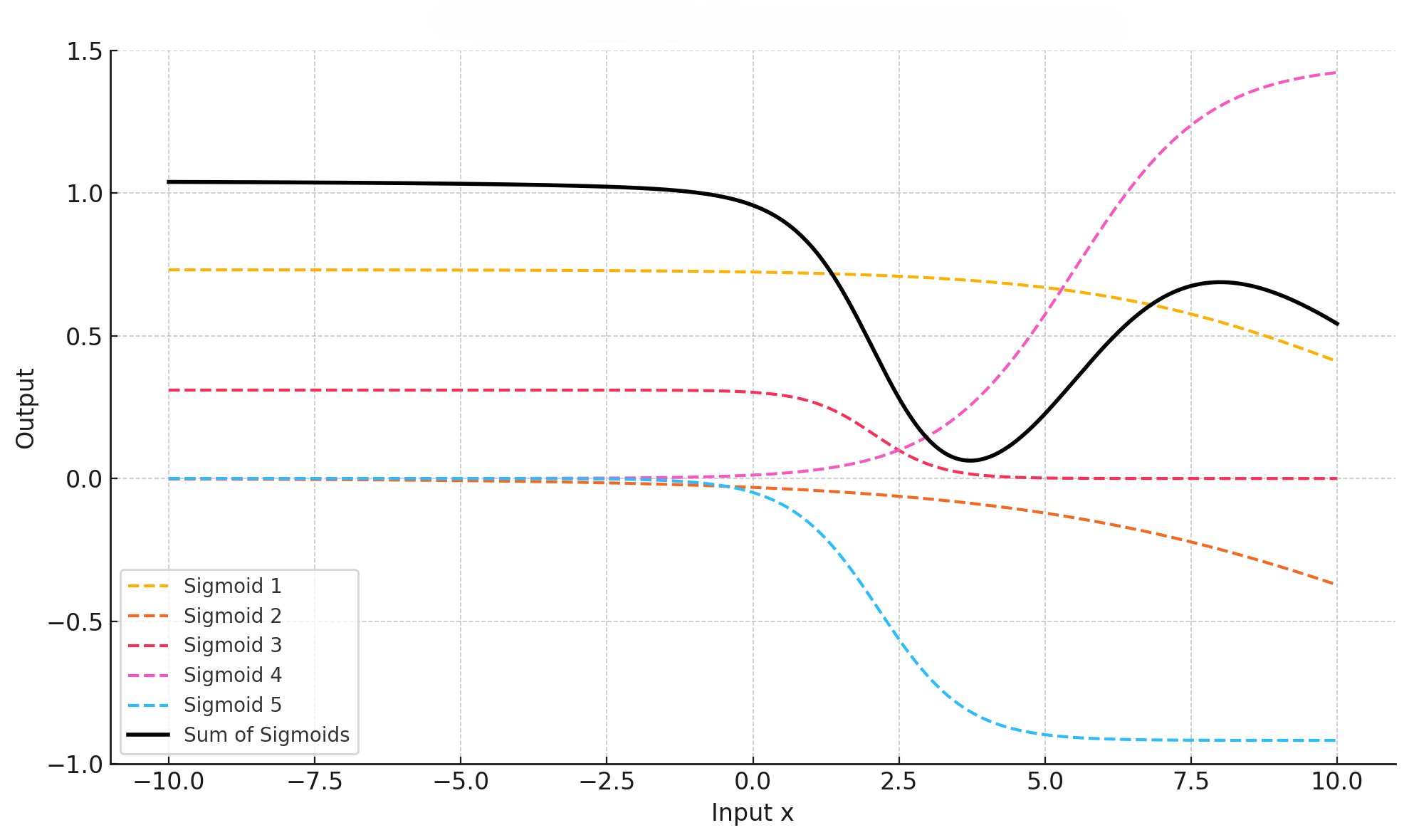
- 第N次迭代:重复第2步的参数优化,经过N轮迭代之后得到精准的函数曲线。

3.数学表示训练过程
3.1.样本数据
-
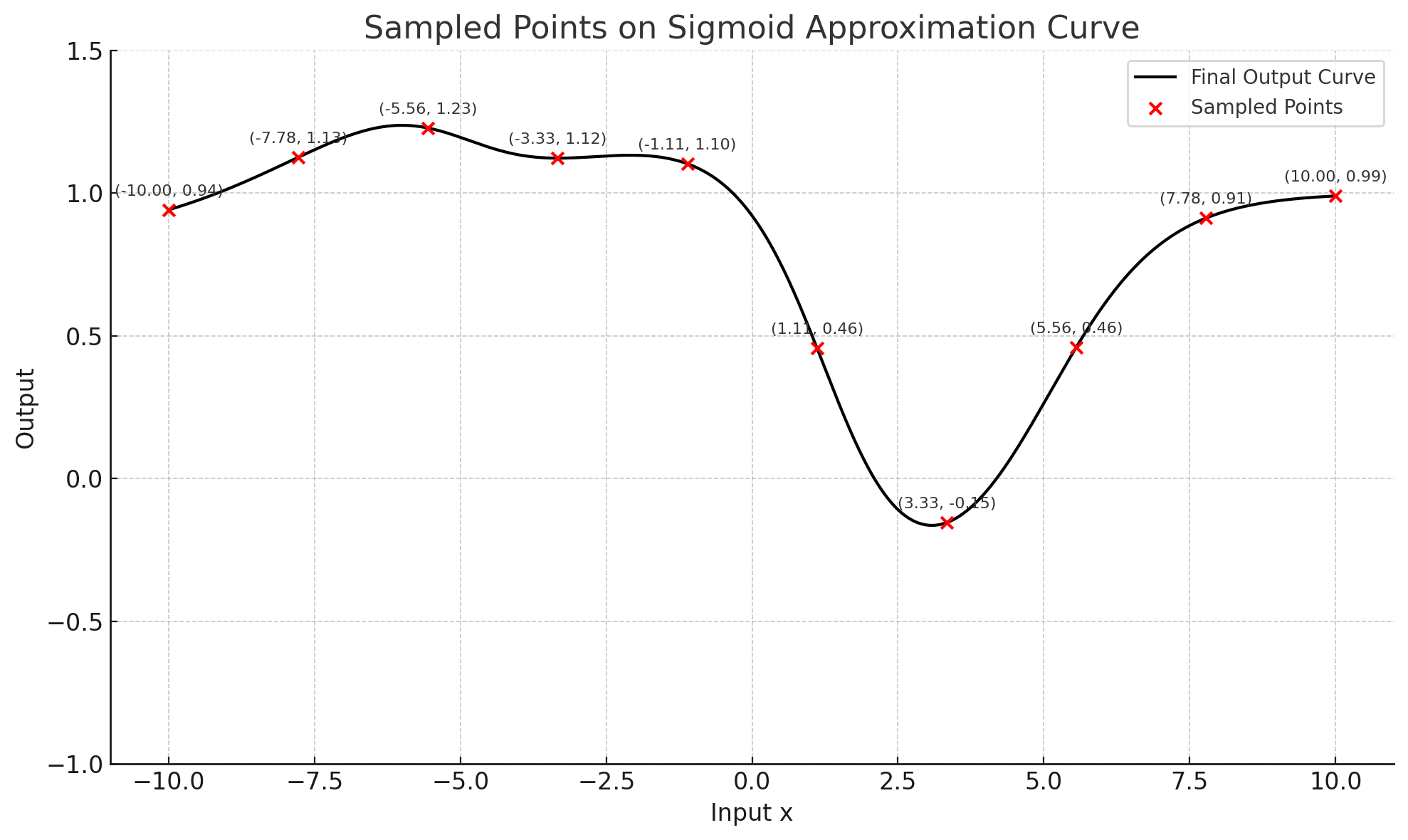
10个(x,y)的样本数据,x:为输入数据有1个特征值,y:为输出的预测数据
[ (-10.0, 0.9413), (-7.78, 1.1254), (-5.56, 1.2278), (-3.33, 1.1222), (-1.11, 1.1027), ( 1.11, 0.4576), ( 3.33, -0.1547), ( 5.56, 0.4595), ( 7.78, 0.9119), ( 10.0, 0.9897) ]
3.2.求解目标
-
最终的目标函数是5个【线性函数+
Sigmoid激活函数】的相加。
\(\sigma\)是
sigmoid函数的简写,\(w_ix + b_i\)是标准的线性函数
$$\tag1 f(x) = \sum_{i=1}^5 a_i \sigma(w_ix+b_i)$$
3.3.设计网络结构
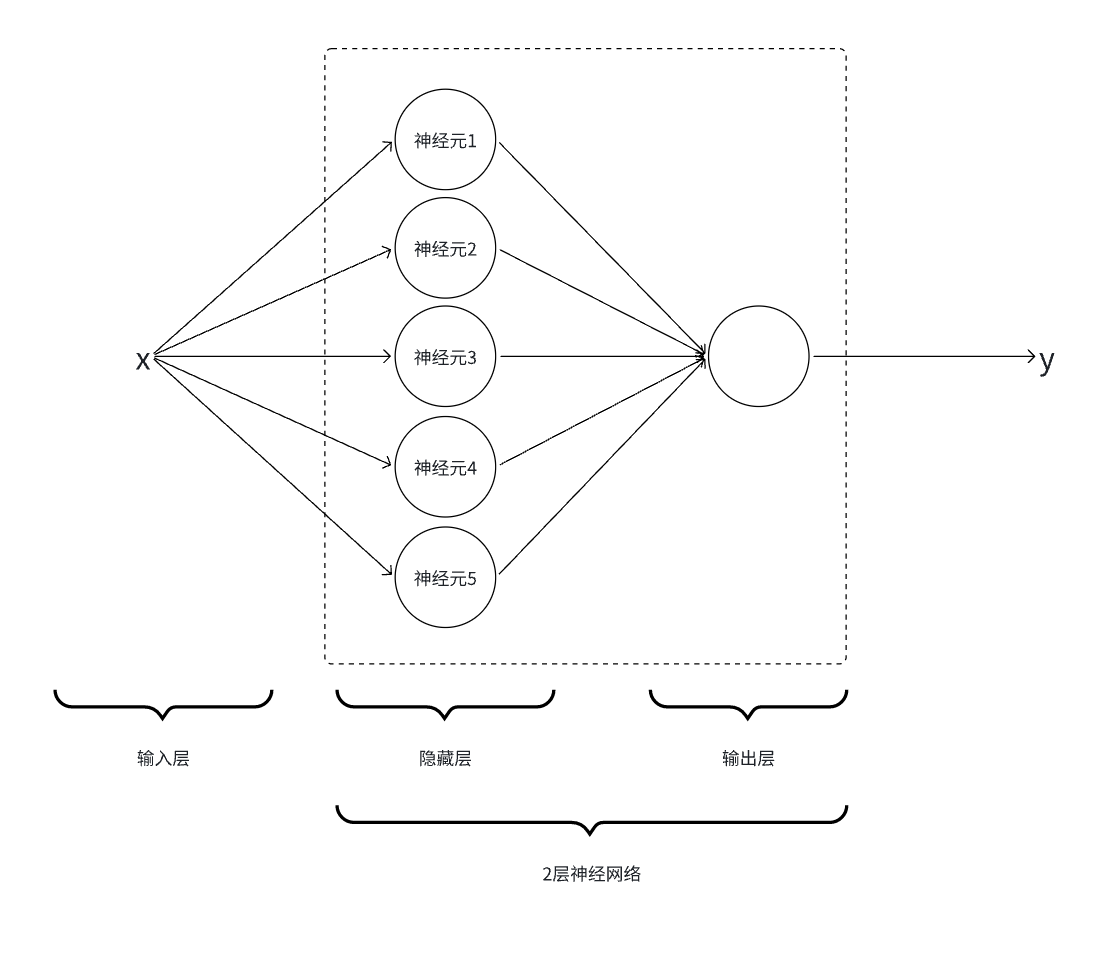
-
隐藏层:5个神经元,即5个【线性函数+
Sigmoid激活函数】
$$\tag1 h_1 = \sigma(w_1x+b_1)$$
$$\tag2 h_2 = \sigma(w_2x+b_2)$$
$$\tag3 h_3 = \sigma(w_3x+b_3)$$
$$\tag4 h_4 = \sigma(w_4x+b_4)$$
$$\tag5 h_5 = \sigma(w_5x+b_5)$$
- 输出层:对隐藏层输出的5个结果进行相加,本质也是线性变换,这里使用简单的权重相加。
$$\tag1 \hat{y} = a_1h_1+a_2h_2+a_3h_3+a_4h_4+a_5h_5$$
- 最终的网络结构(即最终的函数形式):
$$\tag{1} \begin{split} \hat{y} = f(x) = & a_1\sigma(w_1x+b_1) \\\\ + &a_2\sigma(w_2x+b_2) \\\\ + &a_3\sigma(w_3x+b_3) \\\\ + &a_4\sigma(w_4x+b_4) \\\\ + &a_5\sigma(w_5x+b_5) \end{split}$$
- 经过数学建模,求解目标变成:确定函数\(f(x)\)的\(a_i,w_i,b_i\)共15个参数的值。
3.4.迭代训练
3.4.1.训练过程概览
-
第
1轮训练:随机初始化\(a_i,w_i,b_i, i \in [1,5]\) -
第
n轮训练:计算每个参数需要调整的优化量,对上一轮训练的\(a_i,w_i,b_i\)进行优化调整。 -
第
500轮训练:经过500次参数的优化调整得到最终的参数\(a_i,w_i,b_i\)。假设本次训练总次数n = 500。
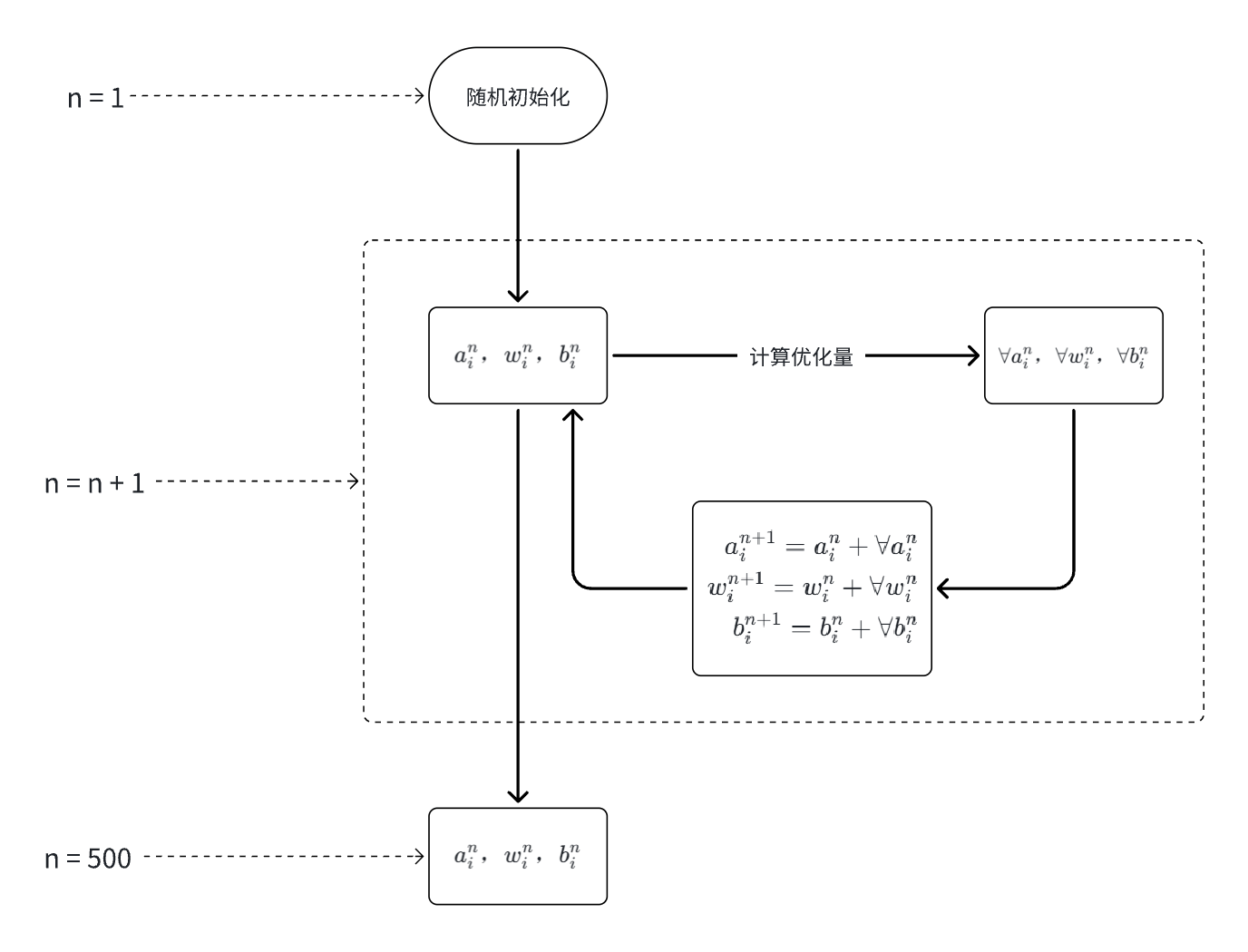
反常识一:
神经网络中,模型的目标并不是求解输入输出\(x\)和\(y\),因为它们在训练数据中是已知的。真正需要学习和优化的是网络中的参数\(a_i,w_i,b_i\)。
反常识二:
神经网络的训练过程并非通过传统的代数方法“解方程”(如多项式求解、方程组消元)获得严格解析解,而是依赖于迭代式的数值优化过程。
因此,神经网络最终得到的参数并不是唯一的解,而是一个在训练数据上表现良好的近似最优解,
3.4.2.损失函数
- 每一轮的训练本质是给参数\(a_i,w_i,b_i\)计算需要的优化值\(\forall a_i,\forall w_i,\forall b_i\)
- 优化值需要满足的条件:每轮训练的预测结果\(\hat{y}\)要尽量接近样本数据的\(y\)
$$\tag1 y – \hat{y} \to 0$$
-
这个函数\(y – \hat{y} \)就是神经网络训练中使用的
损失函数,实际使用中不会直接使用\(y – \hat{y} \)的算数差值,而是使用方差函数。
算术差有诸多不变,如累计多个结果时因为符号导致误差。使用方差可以有效放大局部的差异。
$$\tag1 Loss = (y – \hat{y})^2 \to 0$$
- 求解目标变成:每轮训练需要找到损失函数\((y – \hat{y})^2\)趋近零的每个参数优化量\(\forall a_i,\forall w_i,\forall b_i\)
3.4.3.偏导数
-
我们知道某个
函数变量对函数的偏导数,就是该变量每单位变化引起的函数变化值,即该变量在函数曲线上的斜率 - 所以只需计算每个参数\(a_i,w_i,b_i\)对损失函数\(Loss = (y – \hat{y})^2\)的偏导数,即可得到每轮训练时候参数需要的优化量\(\forall a_i,\forall w_i,\forall b_i\)
- 求解目标变成:计算每个参数对损失函数的偏导数
- 求解目标的演变过程
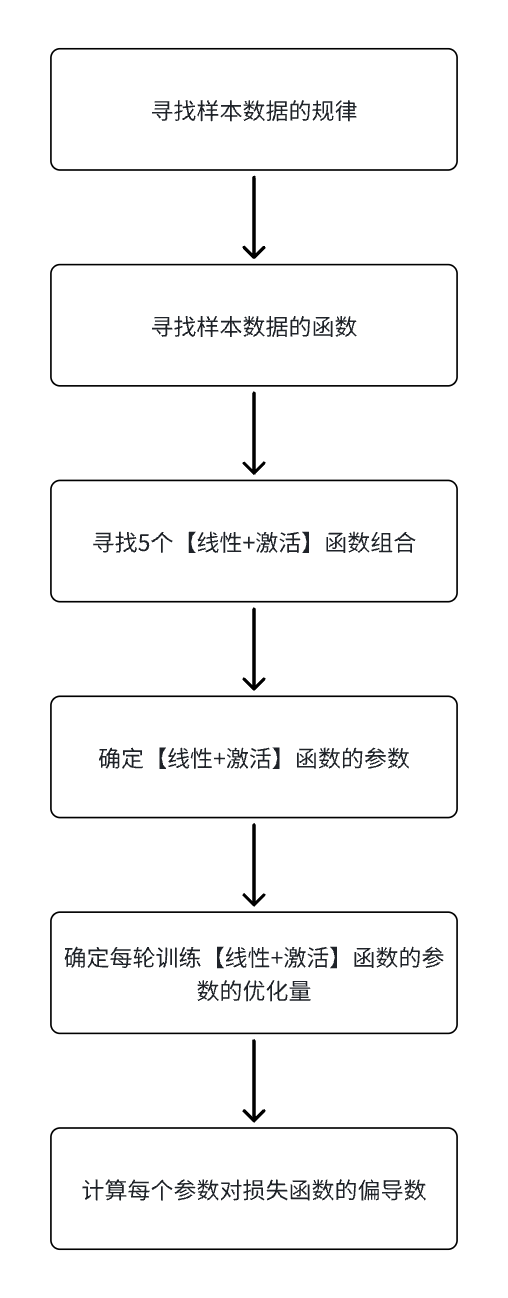
-
链式法则:计算偏导数时需要使用导数计算的链式法则,
x对y求偏导数:
$$\tag1 y = g(f(z(x)))$$
$$\tag2 \frac{\partial g}{\partial x} = \frac{\partial g}{\partial f} \cdot \frac{\partial f}{\partial z} \cdot \frac{\partial z}{\partial x}$$
-
第
n轮训练中参数的偏导数计算
-
- 所有已知的函数
$$\tag{线性函数} z_i = w_ix+b_i$$
$$\tag{激活函数} h_i = \sigma(z_i)$$
$$\tag{线性+激活相加} \hat{y} = \sum_{i=0}^5 a_ih_i$$
$$\tag{损失函数} Loss = (y – \hat{y})^2$$
-
-
a对Loss的偏导数
-
$$\tag1 \frac{\partial Loss}{\partial a} = \frac{\partial Loss}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial a}$$
-
-
w对Loss的偏导数
-
$$\tag2 \frac{\partial Loss}{\partial w} = \frac{\partial Loss}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial h} \cdot \frac{\partial h}{\partial z} \cdot \frac{\partial z}{\partial w}$$
-
-
b对Loss的偏导数
-
$$\tag3 \frac{\partial Loss}{\partial b} = \frac{\partial Loss}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial h} \cdot \frac{\partial h}{\partial z} \cdot \frac{\partial z}{\partial b}$$
-
计算第
n轮训练的参数偏导数,是基于n-1轮的训练结果,所以上述公式中所有的参数\(a^{n-1},w^{n-1},b^{n-1}\)都是已知的。同时样本数据x,y也是已知的。 -
实际使用中
pytorch、tensorflow等框架对求导数做了封装,非常简单就可以实现偏导数的计算。
3.4.4.参数优化量
- 经过计算得到参数的偏导数,再乘于一个自定义的学习率\(\eta\)得到最终的参数优化量。
-
偏导数默认是变量对函数的增长方向,我们的目标是缩小
Loss函数的损失值使其结果趋近0,所以最终参数优化量是偏导数的负数(反方向)。
$$\tag1 \forall a_i = -\frac{\partial Loss}{\partial a_i} \cdot \eta$$
$$\tag2 \forall w_i = -\frac{\partial Loss}{\partial w_i} \cdot \eta$$
$$\tag3 \forall b_i = -\frac{\partial Loss}{\partial b_i} \cdot \eta$$
-
第
n轮训练的参数计算公式如下:
$$\tag1 a^n = a^{n-1} -\frac{\partial Loss}{\partial a_i} \cdot \eta$$
$$\tag1 w^n = w^{n-1} -\frac{\partial Loss}{\partial w_i} \cdot \eta$$
$$\tag1 b^n = b^{n-1} -\frac{\partial Loss}{\partial b_i} \cdot \eta$$
3.4.5.循环迭代
-
假设本次训练
500次,即参数\(a_i,w_i,b_i\)进行500次优化调整(500为自定义值,根据任务而定)
\(a_i\)
-
经过
500次训练迭代,得到最终的参数\(a_i,w_i,b_i\),完成训练。
发表回复